Малдавская пирамида

Существует множество вариаций кубика Рубика. Одна из них это пирамидка вместо куба. В том же журнале «Наука и Жизнь» была опубликована статья по сборке и этой головоломки.

Кстати купить молдавскую пирамидку можно на ozon.ru

Молдавская пирамидка.

Пирамида Рубика

Об этой головоломке журнал сообщил в 1982 году (см «Наука и жизнь» № 7,1982 г.). Тогда она была новинкой и интерес к ней был теоретический: «хороша Маша, да не наша». Теперь пирамидку стали выпускать в большом количестве фабрики игрушек И появился практический интерес: купить купили, а как же ее складывают?

Напомним, о чем говорилось в журнале.

Пирамидка представляет собой геометрическое тело тетраэдр. Как и куб Рубика, она состоит из элементов, которые при повороте граней могут перемешаться с грани на грань. Роль кубиков здесь выполняют маленькие тетраэдры, из которых и сложен большой тетраэдр. У него четыре вершинки (в), 6 реберных элементов, или элементов при основании (о) и 6 средних элементов, расположенных между ними (м). Вокруг любой из четырех осей можно повернуть «вершинку», или «пирамидку»—два яруса сразу.

Расположив тетраэдр какой-либо гранью к себе (фасад), обозначим вершинки подобно тому, как принято для кубика Рубика: В(верх), П (правая), Л (левая) и Т (тыльная).

Теми же буквами обозначают повороты—по часовой стрелке без штриха, а со штрихом — против. Основное движение при решении головоломки — поворот пирамидки, то есть вершинки, вместе со средним слоем.

Основными операциями для приведения пирамиды в порядок были названы: универсальная операция типа ВЛВ’Л'(ПВП’В’, ПЛП’Л’), цикли-чески переставляющая три элементарные пирамидки на двух гранях, и круговая перестановка трех элементов одной грани: П’ЛПЛ’ по часовой стрелке и ВЛ’В’Л —против. Их достаточно для решения головоломки.

А существует ли алгоритм сборки, подобный алгоритму сборки кубика Рубика? — спрашивают читатели.

Предоставляем слово изобретателю «Молдавской пирамидки» инженеру А. А.Ордынцу, который предлагает два способа решения головоломки.

ПЕРВЫЙ СПОСОБ

Поочередное построение граней пирамиды. При этом не обращается внимание на разрушение ранее построенной грани.

Первый этап. Прежде все-го все вершинки в разворачиваются на своих местах так, чтобы цвета сторон совпали с цветом сторон соответствующего среднего элемента и при этом у каждой вершины на каждой стороне образуются ромбики вм, состоящие из двух тре угольников одного цвета. Затем разворачиваются средние элементы м (вместе с вершинками в и реберными элементами о) так, чтобы на каждой стороне пирамиды были ромбики вм только одного цвета (см. 1.2). Три ромбика одного цвета можно построить только на вполне определенной грани. Для облегчения поиска этой грани необходимо исходить из того, что цвет этой грани будет тот, которого нет на противоположной этой грани вершине.

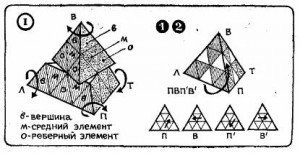
Рисунок 1

Второй этап. После расстановки одноцветных ромбиков на четырех гранях для дальнейшего построения необходимо освоить вспомогательные операции (рис. 1, 2):

а) перевод реберного элемента из основания к вершине В без нарушения построения ромбиков операцией ПВП’В’,

б) подвод на исходную позицию реберного элемента при вершине В с нарушением ромбиков у вершины В операцией В или В’.

Третий этап. Строится основание — нижний слой пирамиды (рис. За, 36). Точкой обозначена сторона реберного элемента, имеющая одинаковый цвет со строящейся гранью, расположенной снизу. Реберный элемент, имеющий цвет строящейся грани, с помощью вспомогательных операций выводится на исходную позицию, при этом допускается нарушение расположения ромбиков у вершины В. Затем в зависимости от положения цветов сторон это-го реберного элемента на исходной позиции применяется одна из операций За или 3 б (ТВ’Т’ или Л’ВЛ). Одинаковой штриховкой на рисунках обозначены треугольники одного цвета. Цвет не заштрихованных треугольников роли не играет. Результат этапа: построено основание — нижний слой, у которого как на грани, обращенной вниз, таки на боковых сторонах основания все треугольники находятся на своих местах.

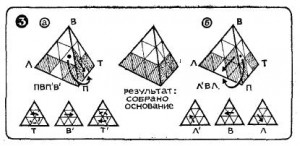
Рисунок 2

Четвертый этап. Поворотом вершины В устанавливаются на свои места ромбики при вершине В, и пирамида переворачивается вниз гранью другого цвета.

Пятый этап. Повторение третьего этапа для построения новой грани. При этом не следует обращать внимание на то, что нарушается порядок элементов на ранее построенной грани.

При необходимости таким же образом строится и третья грань В редких случаях приходится строить четвертую грань, и пирамидка будет собрана.

ВТОРОЙ СПОСОБ

Послойное построение. После построения нижнего слоя — основания — по первому способу (см. третий этап) получится одно из трех возможных положений:

1. Два реберных элемента при вершине находятся на своих местах в развернутом положении. Остальные элементы стоят правильно. Пирамидка собирается процессом: (П’ЛПЛ’) (ВЛ’В’Л).

Рисунок 3

2. Три реберных элемента при вершине стоят не на своих местах. При повороте вершины на 120° они становятся на свои места, однако при этом вершинка и средний элемент неправильно развернуты. В этом случаев зависимости от положения применяются процессы(П’В’П) В’ (П’В’П) или(ПВП’) В (ПВП’).

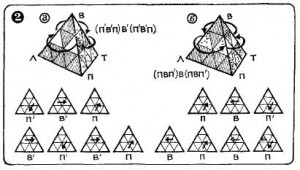
Рисунок 4

3. Три реберных элемента при вершине стоят не на своих местах и развернуты. В зависимости от положения применяются процессы (ПТ’П’Т) (ВТВ’Т) или (П’ЛПЛ’) (В’Л’ВЛ).

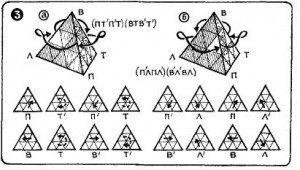
Рисунок 5

Этот способ дает возможность собирать пирамидку за 30 секунд. Возможны, вероятно, и другие пути решения.

«Молдавская пирамидка»допускает построение симметричных узоров на гранях, подобно кубику. Но здесь возможности гораздо скромнее. Задание: используя приведенные процессы перестановки элементов, придумайте алгоритмы построения симметричных узоров.

11 комментариев на “Молдавская пирамидка”