Первый раз в своей жизни я увидел кубик Рубика лет в 9. Долго мучался, крутил его и так и эдак, как правило, получалось собрать только одну грань и частично соседние к ней. Подсунул мне эту головоломку отец и долгое время наблюдал за моими попытками. Но однажды, после очередного моего провала в этот деле, он вспомнил, что в каком-то журнале есть небольшая статейка о том, как его собрать. После недолгого перерывания полок книжного шкафа был найден выпуск журнала «Наука и жизнь». Способ, опубликованный в нём, (метод послойной сборки) я до сих пор считаю самым простым, наглядным и легко запоминающимся. Эту статью я и предлагаю вам для прочтения.
Купить классический кубик Рубика можно на ozon.ru или на my-shop.ru
Маленький совет: в статье написано очень много сложнопонимаемых шифровок, но достаточно понять алгоритм на картинках.
А всё-таки, как его собрать?
«Невозможно иметь изолированный кварк (или антикварк). Кварки не могут существовать свободно, но они могут существовать объединенными в группы: пара кварк-антикварк является мезоном, а трио кварков целым зарядом является барионом…
Возникает вопрос: какая последовательность операций приведет к мезону или бариону, если известно, что возможными являются комбинации кварков исключительно с целой величиной суммы поворотов?..»
Приведенная цитата — не из статьи об элементарных частицах, она взята из статьи о головоломном «венгерском кубике», напечатанной в научно-популярном журнале «Сайентифик американ». «Головоломку века» не обошел своим вниманием, пожалуй, ни один научно-популярный журнал — ни «взрослый», ни «детский». С одной стороны, терминология новейшей физики, употребление понятий математической теории групп, а с другой — соревнования школьников на быстрейшую сборку кубика (эти соревнования даже промелькнули небольшим сюжетом по первой программе центрального телевидения). С одной стороны, наглядная модель для демонстрации сложнейших математических понятий, с другой — демонстрация виртуозного владения геометрическим воображением и логическим мышлением: школьники на ваших глазах собирают куб всего за 30 секунд! (Рекорд — 25,79 сек.). Мне показалось, что ребята с таким же успехом могли бы «работать» и с закрытыми глазами. Нам, конечно, далеко до них, но от этого головоломка не становится менее интересной. Тем более что ею можно заниматься, ставя все новые и новые задачи. Однако прежде всего попробуем выполнить просьбу многих читателей: дать последовательные этапы «сборки» кубика.
Определились два совершенно различных подхода к сборке: «абстрактный» и «конкретный». В первом случае используются многоходовые процессы, которые, казалось бы, не вносят порядка в хаотически разбросанные кубики до последних нескольких ходов. Так поступает М. Тэйстлетуайт — специалист по прикладной математике из Лондона. Он использовал «идеи математической теории групп для компьютерных исследований так называемых превращений особого рода». Вместо того чтобы поставить на свое место, или, как говорят еще, «посадить в седло» определенные классы кубиков, он делает «спуск через подгруппы». Как это он делает, мы не знаем, но суть в том, что сначала с полной свободой делают несколько ходов-поворотов и останавливаются на таких типах ходов, которые впредь будут возможны (разрешены), затем делается еще несколько ходов и опять следует закрепление на каком-либо типе ходов и так далее, пока ограничения не станут такими, что ходов больше сделать нельзя. Это и есть момент полной сборки куба.
Подобное объяснение, пожалуй, сродни известному рассуждению математика о том, как поймать льва в пустыне: «Возьмем пустыню. Поделим ее на две части. В одной— лев, в другой —нет. Ту, в которой лев, снова поделим на две части и так далее, пока область со львом не станет настолько мала, что делить и отбрасывать уже будет нечего: тут и лев! Сплошная абстракция, но тем не менее «лев» оказывается пойманным: Тэйстлетуайту принадлежит мировой рекорд самого короткого алгоритма приведения куба в порядок — всего 52 поворота.
Конкретный или последовательный метод сборки куба более понятен и приемлем для любителей, Д. Макдональд из Стэнфордского университета применяет такой метод: сначала собирается верхний слой без одного углового кубика, место которого (седло, гнездо) вместе с двумя другими седлами вертикального углового ряда используется в качестве «подъездного пути». Два оставшихся слоя собираются посредством перевода кубиков с «подъездного пути» и обратно на него…
Доктор физико-математических наук В. А. Залгаллер (г. Ленинград) дал описание метода, при котором сначала собираются «борта»—12 бортовых кубиков, а затем «углы» — 8 кубиков.
И, наконец, есть ещё метод послойной сборки куба, суть которого состоит в том, что сначала собирается верхняя грань (верхний слой), затем средний слой и, наконец, нижний. После завершения каждого процесса беспорядок уменьшается. Мы получаем ряд последовательно фиксированных состояний куба с постоянно наблюдаемым приближением к упорядоченному состоянию. Но прежде чем перейти к описанию этого алгоритма — несколько замечаний. В статье «Венгерский кубик» («Наука и жизнь» № 3, 1981 г.) мы просили читателей придерживаться в переписке системы обозначений, принятой в журнале. Эта система международная, она нам кажется простой и удобной как для запоминания, так и для записи. Вместе с тем многочисленные зарубежные публикации, а также почта наших читателей позволили внести в систему обозначений некоторые усовершенствования и дополнения. Так, вместо индекса «—1», отмечающего левое вращение грани (против часовой стрелки), будем употреблять индекс «штрих» «’», то естьФ-1 = Ф’.
Рационально во многих случаях отмечать операцию «вращение среднего слоя» С. Например, Сп — вращение среднего слоя со стороны правой грани. Эту операцию удобно выполнять так. Правой рукой поворачиваем на 90° по часовой стрелке сразу два слоя, два «ломтика» — правый и средний, а затем возвращаем на место один правый слой, сделав поворот П’. В результате средний ломтик окажется повернутым на 90° почасовой стрелке. Таким же образом выполняется С-поворот со стороны любой другой грани. Процессы ПЛ’, ВН’ и подобные им, по сути дела, тоже являются поворотом среднего слоя, но с сохранением ориентации центрального кубика и ориентации куба. Иначе говоря, Сп = П’Лх, а С’п =Л’Пх’, где х — элементарная операция «поворота куба на 90° по оси X».
Очень наглядна и удобна матричная форма записи процессов, где элементарные операции-повороты изображаются рисунками фасадной грани, с соответствующими стрелками.
Ячейки матрицы можно использовать при этом для дополнительных пометок.
А теперь собственно о методе послойной сборки. Мы изложим его, ориентируясь на программу, получившую наибольшее распространение.
Первый этап — «верхний крест». На свои места устанавливаются четыре бортовых кубика, принадлежащих верхнему слою. Сориентируем куб так, чтобы впереди оказалась выбранная вами грань, и зафиксируем это.
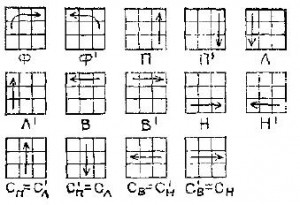
Рисунок 1
Расположение бортового кубика, принадлежащего фасадной и верхней граням в кубе (кубик фв), может быть сведено к пяти основным ситуациям. Сориентировав куб надлежащим образом, выводим нужный кубик на фасадную грань и одной из пяти приведенных операций переводим его на свое место. Выберем для начала фасад синий, верх белый. Тогда справа будет, например, оранжевая грань, слева — красная, сзади — зеленая (цвет зависит от фабричной расцветки куба). Первым кубиком фв, поставленным на место, будет кубик сб — сине-белый. Затем, согласно формулам приведенных операций, ставятся на свои места кубики об, кб и зб оранжевой, красной и зеленой граней. Результатом первого этапа будет крест на верхней грани куба, составленный из четырех бортовых кубиков и центрального кубика грани.
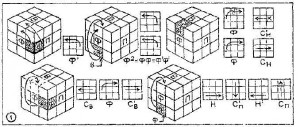
Рисунок 2
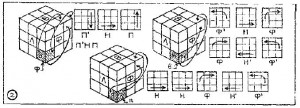
Рисунок 3
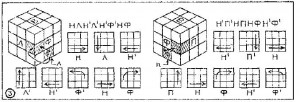
Рисунок 4
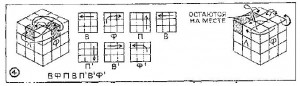
Рисунок 5
Второй этап—«углы верхнего слоя», или просто «углы». Ставим на место кубикифвп, фвл, твп и твл. Выводим на фасадную грань в левый нижний угол нужный кубик, например, фпв — сине-оранжево-белый. Он может занять одно из трех возможных положений. Соответствующим процессом переводим кубик в правый верхний угол. Он займет там свое место и будет правильно ориентирован.
Рисуон 6
Точно так же поступаем, выбрав в качестве фасадной грани не синюю, а оранжевую, зеленую или красную. Верхний слой будет собран полностью.
Третий этап — «пояс» — сборка среднего слоя. Ставим на место его бортовые кубики. В нашем примере, когда вверху белая грань, фасад синий, правая грань оранжевая, это будут кубики: сине-оранжевый, сине-красный, оранжево-зеленый и красно-зеленый. Поворачивая нижний слой, приведем куб к одной из двух стандартных ситуаций, показанных на рисунке: перемещаемый кубик занимает место фн. Обратите внимание: цвет его фасадной грани должен совпадать с цветом центрального кубика фасадной грани куба. В зависимости оттого, какого цвета грань оказалась внизу, переводим этот кубик направо или налево на грань соответствующего цвета одной из двух указанных операций.
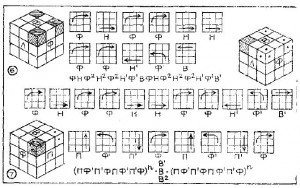
Рисунок 7
Может оказаться, что все четыре искомых кубика находятся в среднем слое, но неправильно ориентированы. В этом случае теми же операциями сначала переводим их в нижний слой, а затем и на свое место.
Четвертый этап — «крест для нижней грани».
Для удобства перевернем куб собранным слоем вниз. Сверху окажутся все кубики несобранного слоя, но не на своих местах. Подберем сначала бортовые кубики». В нашем примере это кубики жс, жо, жз, жк —желто-синий, желто-оранжевый, желто-зе-леный и желто-красный.
Возможно использование различных процессов, но с одним ограничением: не разрушать уже собранные два слоя. Такому ограничению соответствуют, например, два процесса, один из которых меняет местами два кубика, а другой — переворачивает нужный кубик.
В первом случае два указанных на рисунке кубика не только меняются местами: один из них (верхний левый) еще и переворачивается, меняя ориентировку.
Если верхняя грань желтая, фасад синий, слева — оранжевая грань, то в ситуации «впереди кубик оранжево-желтый (желтой гранью вверх), а слева вверху желто-синий (синяя грань вверху)», этот процесс поставит оба кубика на свои места. При этом будут затронуты еще 4 кубика того же слоя, но на данном этапе это не должно нас волновать. Однако здесь надо заметить: выбор цвета фасадной грани (ориентация куба) перед началом четвертого этапа производится с учетом того, что кубик тв остается на месте, а кубик пв, оставаясь на месте, меняет ориентировку. Кубики фви лв меняются местами, причем фв сохраняет ориентацию, а лв «опрокидывается».
Возможно, что операции 4-го этапа придется проделать два — четыре раза, пока все 4 кубика не сядут в свои гнезда. При этом может оказаться, что все четыре ориентированы неправильно, или два кубика окончательно стали на свои места, а два других, хоть и займут места в своих гнездах, но будут неверно ориентированы.
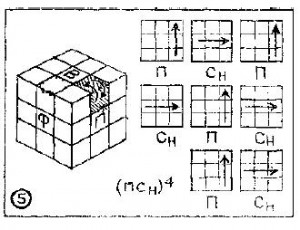
Правильной ориентации их можно достигнуть с помощью процесса (ПСН) 4.
Пятый этап — «ориентация бортовых кубиков последней грани».
Расположим куб так, чтобы любой из неверно ориентированных кубиков оказался справа вверху (занял гнездо пв). Сделаем 8 указанных поворотов. Кубик должен развернуться и стать правильно. Не огорчайтесь, что нарушился порядок в ниже лежащих слоях: все будет исправлено. Поверните верхнюю грань (только верхнюю грань, а не весь куб!) так, чтобы место справа вверху занял другой неверно ориентированный кубик, и повторите указанный процесс. Второй кубик займет правильную позицию, а нижние слои вновь будут упорядочены.
В результате на верхней грани будет собран крест — бортовые кубики окажутся на своих местах. Проверьте совпадение цвета слоев по всему кубу, возможно, придется повернуть верхнюю грань.
Шестой этап — «углы последней грани».В результате предыдущей операции может оказаться, что ни один угловой кубик не займет своего места. Тогда все четыре надо переместить в свои гнезда, пусть и неправильно ориентированно. Этого можно достичь 22-ходовым процессом. Проделайте его. Если ни один кубик при этом еще не уселся в свое гнездо, то следует повторить процесс.
Как только вы увидите, что какой-либо угловой кубик сел на свое место и правильно сориентировался, поверните куб так, чтобы этот кубик оказался на тыльной грани слева (см. рис.). Теперь можно снова повторить 22-ходовую операцию один, а возможно, и два раза.
Седьмой этап — «ориентация угловых кубиков последней грани».
Кубики заняли свои гнезда. Но два из них или даже все четыре могут оказаться не с ориентированными.
Указанный 8-ходовой процесс поворачивает «плохой» кубик, помещенный в правый угол фасадной грани по часовой стрелке на 1/3 оборота, и возможно, что этот процесс придется повторить еще раз. На рисунке это отражено индексом «n».
Внимание! Процесс затрагивает все слои куба — не ошибитесь, иначе все придется делать с самого начала. Чтобы развернуть следующий кубик, его надо сначала поворотом одной лишь верхней грани (операцией В’, В или В2) поместить в правый верхний угол фасада и вновь повторить восьмиходовку. Теперь остался всего один «плохой» кубик. Поворачивая лишь верхнюю грань, поместите его в правый верхний угол и снова тем же процессом (8 или 8×2 ходов) сориентируйте его. Остался заключительный ход: поворот верхней грани, и все — куб собран.
Предложенный алгоритм не единственный. Вот некоторые предложения, взятые нами из читательской почты.
Е., Н. и В. Довгошей (г. Ужгород) сообщают, что у них в городе получила распространение такая система упорядочения кубика.
1. Процессом Ф’В’П’Ф’ПФВ, аналогичным описанному в операции четвертого эта-па, выставляют в свои гнезда все 12 реберных кубиков, пока без учета их ориентации. Не обращают внимания и на миграцию угловых кубиков.
2: ПроцессомП2Ф2П2Ф2ПВ’П2ВФПВФ2В’Ф (А6)
или ФП’Ф’П2В’П’В2Ф’В’Ф (А’6)
выполняется ориентация реберных кубиков. Процесс А’6 на 8 ходов меньше процесса А6, разработанного с помощью ЭВМ, но приводит к тем же результатам.
Рисунок 8
3. Угловые кубики перемещают операциями, не затрагивающими реберные кубики. Это процессы, затрагивающие две грани.
(ВФВ’Ф’) 3 (А2)
или (ФПФ’П’) 3— кому как удобнее вращать грани куба.
Или процесс Л’В’П’ВЛВ’ПВ (А7),
затрагивающий лишь одну грань (см.«Наука и жизнь» № 3, 1981 г.).
Тот же результат, что и А7, дают процессы(ВФВ’Ф’)3 (П’Ф’ПФ)3 А17 и (П’Ф’ПФ)3 (ВФВ’Ф’)3 А’17 они длиннее, но более удобны для запоминания.
Рисунок 9
4. Ориентация угловых кубиков. Пользуясь многократно одним процессом (ФП’Ф’П2В’П’В2Ф’В’Ф)2 А18 поворачивающим на 1/3 оборота (кварк!) против часовой стрелки три угловых кубика одной грани и обратным ему, можно правильно сориентировать все 8 угловых кубиков.
Рисунок 10
Судя по всему, в Ужгороде распространилась программа сборки куба, описанная в журнале «Квант» ленинградцами д-ромф.-м. наук В. А. Залгаллером и А. Залгаллер. Кандидат физ.-мат. наук В. Н. Кузовков (г. Рига) сообщил о разработанной им программе послойной сборки куба. Сначала собирается нижний слой. Для сборки второго слоя используются операции
Ф2В2ФВ2Ф2 А19
Ф2В2Ф’В2Ф2 А20
Рисунок 11
на последней стадии этого этапа применяется процесс
(Ф’В’ФВ2)2Ф’ВФ A21
а также (ПВП’В2)2ПВ’П’ А22.
Рисунок 12
Оба процесса заменяют только один кубик пф во втором слое и не затрагивают собранного нижнего слоя.
Поворот кубика фп осуществляется процессом
(ПВ2П’В)2Ф’В’Ф А23.
Рисунок 13
Для упорядочения последнего слоя предложен «блочный» метод, использующий две группы процессов
ПВП’Ф’ Вn ФПВ’П’ А24
и Ф’В’ФП Вn П’Ф’ВФ А25
где Вn означает поворот верхней грани на 90°, 180° и 270° (—90°).
Комбинируя сочетание этих двух процессов с операциями В, В1 и В2, можно поставить на место и правильно сориентировать все кубики верхней грани.
Интересно было бы разработать более короткие программы сборки последней грани, хотя бы для каких-то конкретных случаев, с которыми приходится иметь дело. Скажем, поменять местами два противолежащих бортовых кубика и одновременно два угловых, то есть придумать процессы, аналогичные алгоритмам А4, А11, А12 приведенным в журнале «Наука и жизнь», № 3,1981 г.
А. В. Гусев (г. Дубна) для сборки первого и второго слоя рекомендует те же процессы, что и В. Н. Кузовков. Для сборки последнего слоя он применяет операции
ФПВП’В’Ф’ А26
для разворота бортовых кубиков и перестановки угловых кубиков попарно вдоль граней с разворотом их
ПВ2П’В’ПВ’П’ А27
для установки бортовых кубиков на свои места без их разворота, а также перемещения угловых кубиков попарно из угла в угол по диагонали
П’Ф’Л’ФПФ’ЛФ А28
и ЛФПФ’Л’ФП’Ф’ А29
для перемещения трех угловых кубиков(ПВ’П’В’Ф’ВФ)4 А30
Рисунок 14
для разворота угловых кубиков в конце сборки, согласно таблице разворотов.
В этой таблице приведены 7 возможных вариантов положения угловых кубиков верхней грани:
о — кубик ориентирован правильно
+ — кубик следует повернуть на 1/3 почасовой стрелке
— — кубик надо повернуть на 1/3 против часовой стрелки.
Варианты 2, 4, 5 процессом А30 сводятся к варианту 1. Варианты 3, 6, 7 — сначала к варианту 2, затем — к варианту 1, а последний приводит процессом А30 к полной сборке куба.
Интересные разработки и решения задач содержатся также в материалах, присланных В. В. Перетрухиным (Москва, МГУ)Л. И. Шлейфманом (Москва, МРИ),Г. А. Кимом (Москва, МИС и С), Э. Э. Рестиным (г. Рига), Г. Константиновым (г.Удомля), А. И. Сотниковым (г. Львов),Л. И. Ивановым (г. Москва), А. Лиепиньшем (г. Рига), В. Маркиным (г. Тамбов).
А теперь обратимся к 8-й странице цветной вкладки.
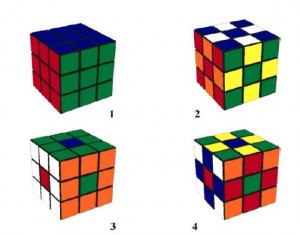
Рисунок 15
В журнале «Наука и жизнь» № 3, 1981 г.был приведен алгоритм построения «шахматного кубика» за 36 поворотов. Многие читатели сообщили, что эту фигуру они построили не за 36, а всего за 6 двойных поворотов; Ф2Л2П2Н2В2Т2.
Добавим: если вращать средний слой, то понадобится всего три двойных поворота СП2 СВ2 СФ2
Интересно, что фигура «шахматный кубик» (2) получила название «Pons Asinorum» («Ослиный мостик»). Дескать, кто смог найти алгоритмы построения этой фигуры самостоятельно, может заниматься кубиком и дальше, а кто не смог перейти этот мостик… пусть пеняет на себя. Но вот вопрос: сколько различных способов существует для построения «Ослиного мостика»?
И еще. На цветной вкладке показаны кубики, полученные путем поворота его граней примечательные фигуры: 1. Расцветка исходного куба. Фасад — красный, верх —синий; правая грань—зеленая, левая —желтая, тыл — оранжевый, низ—белый;2. Ослиный мостик. 3. Точки.
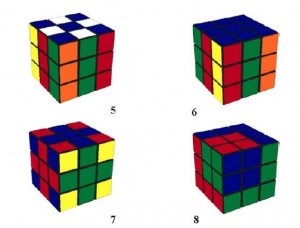
Рисунок 16
4. Ослиный мостик с точками. 5. Столбики. 6. Столби-ки с крышей. 7. Крест Кристиана. 8. Гигантский мезон. 9. Четыре Z. 10. Шесть Н.11. Гигантский мезон с вишнями. 12. Кварк антикварк. Приводятся алгоритмы построения фигур. Обратите внимание, что операции поворота среднего слоя и поворот всего куба не применяются: чтобы не запутаться, фасад, правая и верхняя грань не меняют ориентации при поворотах граней.
Внизу справа (12) —цветное изображение куба другой расцветки. Так он выглядит на экране дисплея электронно-вычислительной машины. В правом верхнем углу куба, если красную грань принять за фасадную, один кубик повернут на 120° (на 1/3оборота) по часовой стрелке (кубик фпв),а все остальные — на своих местах. Такую конфигурацию получить невозможно. Используя терминологию физики элементарных частиц, кубик назвали «кварком». Однако если в противоположном углу имеется кубик (тлн). повернутый на 1/3 оборота против часовой стрелки (антикварк), то такой куб может существовать.
Графическое изображение куба на экране дисплея получено Б. Гринбергом и Д. Кристианом (Массачусетский технологический институт). Разработанная программа позволяет видеть куб в любой момент, с любого угла любой грани в процессе выполнения любого заданного поворота.
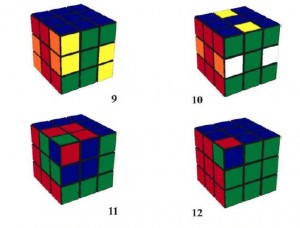
Рисунок 17
Естественно, с помощью такой программы можно разрабатывать последовательности превращения позиций.
У большинства наших читателей такой возможности нет, но все фигуры, приведенные на цветной вкладке, можно получить вручную, если быть достаточно терпеливым и внимательным.
Последняя тройка — позиции 10, 11 и .12 — задачи. Если вам удастся построить фигуру «кварк-антикварк» (12), то вы легко решите задачу 11 — «Гигантский мезон с вишнями», так как эта конфигурация получается разворотом кубиков фвп и нтл в гигантском мезоне (8), а его алгоритм приведен на вкладке. Для решения задачи«Шесть Н» (10) у вас тоже есть все необходимые данные.
И. Константинов. «Наука и жизнь» 1982 г, № 2, стр. 97
P.S. Для тех кто дочитал таки до конца прикладываю pdf файлик с другой статьёй из этого же журнала с более хорошими рисунками NiG(1983-05)p104.



Самый нерациональный и самый трудный метод сборки — это послойный , где сложность сборки возрастает с каждым собранным слоем. Неужели, это не очевидно и надо объяснять, что профессор и математик Давид Сингмастер, не создавал самый простой метод, а просто доказал всем, как с помощью математической теории групп и программистов, можно собирать кубик по слоям. Нотация, формулы, алгоритмы — это всё очень просто, особенно для начинающих.
А как же мне быть, если я собрал его за два вечера, без всяких формул и алгоритмов, продолжать считать, что самый простой — это послойный метод, а я наверное неправильно кубик собираю. Посоветуйте, что делать, может начать учить послойный метод.
не ориентируется угловой кубик последней грани. кто подскажет как исправить ситуацию.
А как же мне быть, если я собрал его за два вечера, без всяких формул и алгоритмов, продолжать считать, что самый простой — это послойный метод, а я наверное неправильно кубик собираю. Посоветуйте, что делать, может начать учить послойный метод.
Объяснить людям Раз такой умный, а не выступать…
Сложность возрастает-ерунда. Средней руки методика. Я три похожих свободно
применяю по памяти…
А вообще никого не заботит кто как кубики на свои места ставит.
P.S. Для тех кто дочитал таки до конца прикладываю pdf файлик с другой статьёй из этого же журнала с более хорошими рисунками.
MY P.S.
Это кстати Одна из замечательных подобных методик с описанием.