iPuzzles

Всё таки решить эту головоломку сможет почти каждый. Главное выбрать себе уровень сложности по плечу. Судоку интересная головоломка, хорошо занимающая сонный мозг и свободное время. В целом любой, кто пытался её решить, уже сумел выделить некоторые закономерности. Чем больше её решаешь, тем лучше начинаешь понимать принципы игры, но и тем больше хочется как-то улучшить свой способ решения. Со времени возникновения судоку люди разработали уже множество различных способов решения, какие-то проще, какие-то сложнее. Ниже приведён примерный набор базовых подсказок и несколько из наиболее простых методов решения судоку. Для начала определимся с терминологией.

Искушённые любители могут купить настольную версию судоку на ozon.ru

Терминология

• Клетка это базовый элемент судоку, в котором должна находиться цифра от 1 до 9. Каждая клетка является частью трех групп одновременно: одного ряда, одной колонки и одной области.
• Группы
  • Ряд состоит из 9 клеток, расположенных по горизонтали.
    
  • Колонка состоит из 9 клеток, расположенных по вертикали.
    
  • Область состоит из 9 клеток, расположенных в области 3х3, кроссворд состоит из 9 таких областей.
• Сегмент − это три клетки внутри одной области расположенные по вертикали или по горизонтали. Каждая область таким образом содержит 6 сегментов, и каждый ряд или колонка содержит 3. Сегмент является частью одновременно области и ряда, или области и колонки.
• Кандидаты − это возможные варианты цифр для данной клетки. Они показаны маленьким шрифтом. Когда в клетке остается только один кандидат, это число может быть размещено в клетке. Если в клетке два кандидата —  это пара, три — трио, четыре — квартет.

Далее, перечислим несколько способов в порядке возрастания сложности.

Способ 1: Синглы

Синглы (единственные варианты) могут быть определены исключением цифр, уже присутствующих в рядах, колонках или областях. Следующие методы позволяют решить большинство «простых» вариантов судоку.

1.1.Очевидные синглы

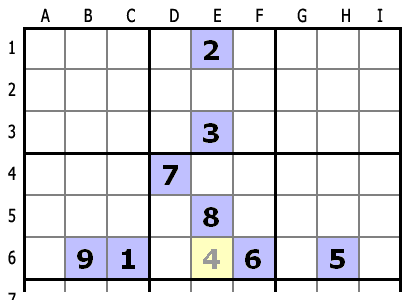Число может быть назначено в клетку когда оно является единственным вариантом, принимая во внимание ряд, колонку и область, содержащие эту клетку.

В клетке E6 единственный возможный вариант это 4, т.к. остальные числа уже содержатся в группах, содержащих клетку (ряду, колонке и области).

1,5,6,9 могут быть исключены, т.к. они уже находятся в ряду. 2,3,8 могут быть исключены, т.к. они уже находятся в колонке. 6,7,8 могут быть исключены, т.к. они уже находятся в области. Таким образом 4 остается единственным кандидатом.

1.2.Скрытые синглы

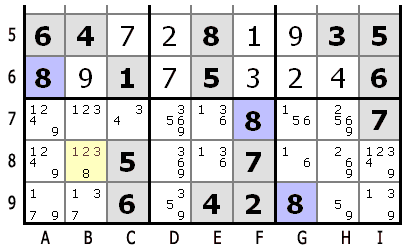Когда клетка является единственной в группе, которая может содержать число, это число должно быть назначено ей.

Рассматривая кандидатов для группы, если одно число появляется только в одной клетке, даже если в ней есть другие кандидаты, проставленные методом 1.1, тогда эта клетка должна содержать это число.

В 7-й области (нижней левой) число 8 возможно только в центральной клетке B8. Таким образом мы можем исключить кандидатов 1,2 и 3 и назначить этой клетке число 8.

Число 8 уже находится в 7-м ряду в F7, в 9-м ряду в G9 и в колонке A в A6. Поскольку в клетке C8 уже находится число 5, только B8 может содержать 8 в этой области.

Способ 2: Исключение кандидатов

Предыдущие методы позволяли окончательно назначить число в клетку.
Следующие позволяют уменьшить возможных кандидатов в клетке для того, чтобы в будущем найти единственное значение для клетки.

2.1. Сегмент 1

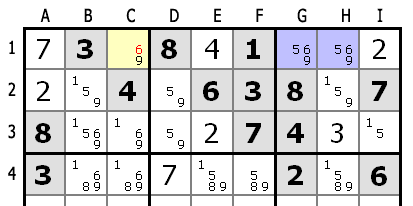Если в области число возможно только в одном сегменте, то кандидат может быть исключен из этого ряда или колонки в других областях.

В 3-ей области (верхней правой), число 6 возможно только в верхнем сегменте (G1 и H1). 6 должно быть в первом ряду этой области. Таким образом 6 может быть исключено из кандидатов в клетке C1.

В 3-ей области число 6 не может находиться во втором ряду, т.к. оно уже есть в клетке E2. Оно также не может находиться в третьем ряду, т.к. там уже назначены два числа (4 и 3), и 6 уже находися в колонке I, в I4.

Простыми словами: если точно не известно место цифры, но есть две клетки в области, где она может находится, и они все лежат на столбце или строке, то эту цифру можно вычеркнуть из кандидатов по этой строке или столбцу соответственно.

2.2. Сегмент 2

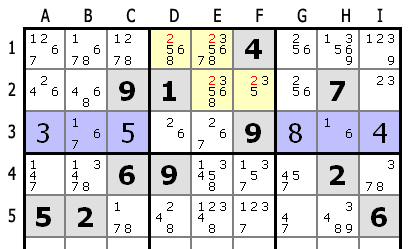Когда в ряду или колонке только одна область может содержать число, это число должно быть исключено из кандидатов в других клетках этой области.

В 3-м ряду только вторая область может содержать число 2 (в D3 или E3). Следовательно, 2 не может быть назначено в клетки первого и второго ряда этой области.

Принимая во внимания числа, уже назначенные в 3-м ряду, а также те, которые назначены в колонках B и H, число 2 может находиться во второй области только в третьем ряду. Таким образом 2 может быть исключено из D1,E1,E2 и F2.

Способ 3: Группы кандидатов

3.1. Очевидные группы кандидатов

Когда группа содержит две клетки с одинаковыми парами кандидатов (также единственными), тогда эти кандидаты не могут находиться в других клетках этой группы. Это можно применить к ряду, колонке или области.

Во втором ряду в клетках G2 и H2 кандидатами является пара 1,4. Если в G2 находится 1, то в H2 будет 4, и наоборот. В любом случае эти две клетки обязательно будут содержать 1 и 4. Таким образом мы можем исключить этих кандидатов из остальных клеток ряда.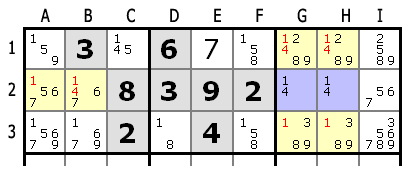

Поскольку эти пары обе находятся в третьей области (правой верхней), мы также можем исключить числа 1 и 4 из остальных клеток этой области.

Когда три клетки в одной группе не содержат иных кандидатов кроме трех, эти числа могут быть исключены из остальных клеток группы.

Обратите внимание: не обязательно, чтобы эти три клетки содержали все числа трио! Необходимо только чтобы эти клетки не содержали других кандидатов.

В этом ряду мы имеем трио 1,4,6 в клетках A, С и G, или двух кандидатов из этого трио. Эти три клетки будут обязательно содержать всех трех кандидатов. Поэтому они не могут быть в другом месте в этом рядом, и поэтому могут быть исключены из других клеток (E и F).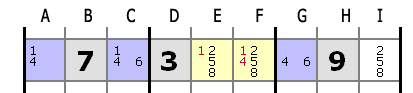

Аналогично для квартета, если четыре клетки не содержат иных кандидатов кроме как из одного квартета, эти числа могут быть исключены из других клеток этой группы. Как и для трио, клетки, содержащие квартет не обязаны содержать всех четырех кандидатов квартета.

И так далее, для N кандидатов в группе, мы можем найти N клеток, которые содержат только этих кандидатов. После этого мы можем исключить эти числа из остальных клеток группы.

3.2.Скрытые группы кандидатов

Для очевидных групп кандидатов (предыдущий метод: 3.1) пары, трио и квартреты позволяли исключить кандидатов из других клеток группы.
В этом методе, скрытые группы кандидатов позволяют исключить других кандидатов из содержащих их клеток.

Если есть N клеток (2,3 или 4), содержащие N общих чисел (и они не встречаются в других клетках группы), тогда остальные кандидаты для этих клеток могут быть исключены.

В этом ряду пара (4,6) встречается только в клетках A и C.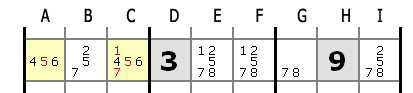

Остальные кандидаты, таким образом, могут быть исключены из этих двух клеток, поскольку они должны содержать либо 4 либо 6 и никаких других.

Как и в случае очевидных трио и квартетов, клетки не обязаны содержать все числа из трио или квартера. Скрытые трио очень сложно рассмотреть. К счастью, они не часто используются для решения судоку.
Скрытые квартеты разглядеть практически невозможно!

Правило 4: Сложные методы.

4.1. Связанные пары (бабочка)

Следующие методы не обязательно более сложные для понимания чем вышеописанные, но не так просто определить когда они должны применяться.

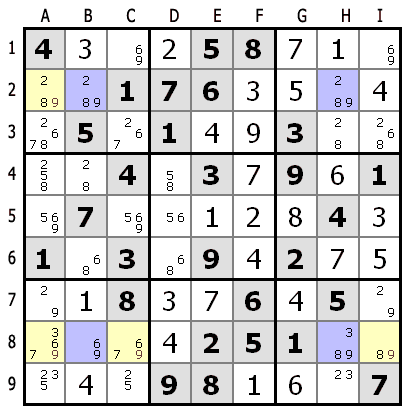Если какое-то число возможно только в двух ячейках двух рядов, и эти 4 варианта находятся в двух колонках (и формируют прямоугольник), тогда этот кандидат может быть исключен из других клеток колонки.
Аналогичный метод применяется в случае двух колонок, исключаемые кандидаты тогда будут в рядах.

Для колонок B и H, 9 возможна только во 2м и 8м рядах (голубые клетки). Таким образом 9 может быть исключена из остальных клеток этих рядов.

Для колонки B, если 9 находится не в B2, она будет в B8 и наоборот для колонки H. Таким образом 9 будет обязательно в 9м или 2м ряду, либо в B2 и H8, либо в B8 и H2.

Так что 9 может быть исключена из остальных клеток этих рядов.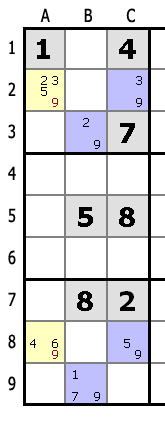

Этот метод может применяться к областям:

Как и в предыдущем примере, две колонки (B и C), где 9 может быть только в двух ячейках (B3 и B9, C2 и C8).

Поскольку B3 и C2, как и B9 и C8 находятся внутри одной области (а не в одном ряду, как в предыдущем примере), 9 может быть исключена из остальных клеток этих двух областей.

4.2 Сложносвязанные пары (рыба)

Этот метод является более сложным вариантом предыдущего (4.1 Связанные пары).

Вы можете применить его когда один из кандидатов присутствует не более чем в трех рядах и во всех рядах они находятся в одних и тех же трех колонках.

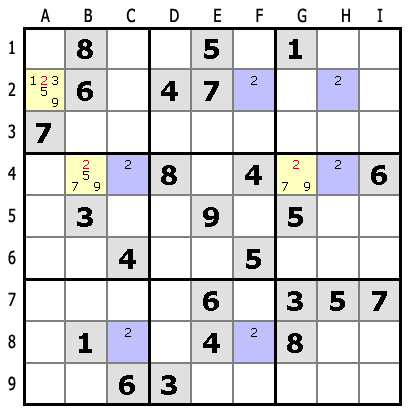Кандидат тогда может быть исключен из остальных рядов этих трех колонок. Тот же метод применяется в случае трех колонок, тогда кандидаты будут исключаться из рядов:

В колонках C, F и H, 2 встречается только в двух клетках. Эти клетки находятся в трех рядах, 2м, 4м и 8м.

Во 2м ряду число 2 будет обязательно или в F2 или в H2, в 4м — в C4 или H4, и в 8м — в C8 или F8.

Таким образом мы можем исключить 2 из остальных клеток этих рядов (в данном примере это отмеченные желтым клетки A2, B4 и G4).

4.3. Связанные кандидаты

Когда число возможно только в двух клетках группы (ряда, колонки или области), эти два кандидата связаны друг с другом.

Если один верен, то другой нет, и наоборот.
Когда несколько пар таких связанных кандидатов соединены, то иногда возможно исключить число из другой клетки, поскольку независимо от того, окажется связанный кандидат верным или нет, в нашей клетке он точно не появится.

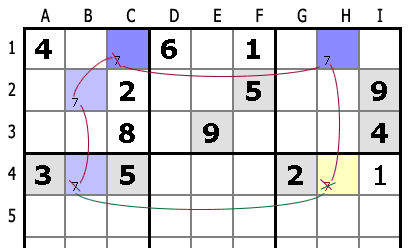В колонке B число 7 возможно в B2 и B4. Это связанная пара, т.к. если B2 верно (7 находится в B2), то B4 — нет, и наоборот.

Аналогично для C1 и H1 в первом ряду, если один кандидат верен, то другой нет.

Эти связи кандидатов объединены в первой области.

Если 7 находится в B4, тогда она может быть исключена из H1. И если она не находится в B4, тогда она находится в B2, не находится в C1, находится H1, и опять же не находится в H7.

В любом случае 7 не может находиться в H1.

4.4. Цепочки

Этот метод может использоваться когда большое количество клеток содержит только двух кандидатов.

Выбирая одного из кандидатов в начальной клетке, Вы формируете цепочку выборов, которая приводит к удалению кандидата в некой клетке.

Если при выборе другого кандидата в начальной клетке Вы приходите к удалению того же кандидата, он может быть спокойно удален.

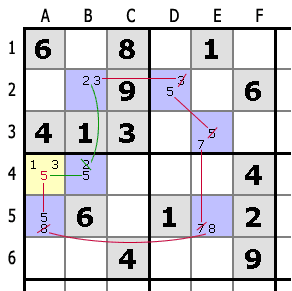Начиная в B2, если 3 верно, то выполняется цепочка заключений (показана красным):

B2 : 3, D2 : 5, E3 : 7, E5 : 8, A5 : 5, таким образом 5 не находится в A4

Если же в B2 находится 2, тогда мы имеем (показано зеленым):

B2 : 2, B4 : 5 и опять 5 не находится в A4.

В любом случае кандидат 5 может быть исключен из клетки A4.

Правило 5: Предположения

Иногда невозможно продвинуться в решении судоку используя один из вышеперечисленных методов.

Тогда Вы можете выбрать кандидата в клетке и посмотреть, к чему приводит такой выбор…

Если рассуждения заканчиваются тупиком или невозможной ситуацией, тогда мы должны вернуться к начальному предположению и попробовать другой вариант.

Такой метод предполагает гадание и обычно не используется при решении судоку.

Информация взята с хорошего сайта, посвящённого судоку и не только, dumaidumai.ru.

20 комментариев на “Как решить судоку?”